Selbstlernkurse für Mathematikdetektive
Abschnittsübersicht
-
-
Selber Zaubern lernen und andere verblüffen, das ist für jeden ein großer Wunsch.
Zaubern bietet vielfältige Lernchancen, die sich durch das Anwenden „verborgener“ Rechenregeln und Gesetzmäßigkeiten darstellen.
Entdecke, wie und warum die Tricks funktionieren und welche Zusammenhänge erkennbar sind.-
Gemeinsam werden wir den 1. Zaubertrick erarbeiten. Hier öffnet sich die Animation.
Klicke zum Starten der Animation auf das grüne Fähnchen.
Über deine Tastatur kannst du die Antworten eingeben.
Klicke nach der Eingabe immer auf Enter.
-
-
abgeschlossen
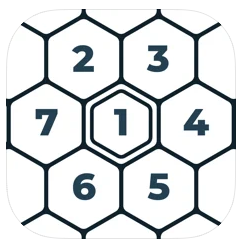
Arithmagone sind Vielecke, deren Ecken und Kanten mit Zahlen beschriftet sind.
Jede Kantenzahl ergibt sich aus der Summe der benachbarten Eckzahlen.Du kennst Arithmagone aus deinem Mathematikbuch. Arithmagone können Rechendreiecke, Rechenvierecke oder sogar Rechenvielecke sein.
-
abgeschlossen
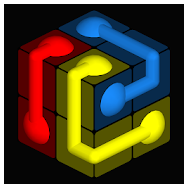
Seit tausenden von Jahren lassen die Menschen den Würfel entscheiden. Damit gehört der Würfel zu den ältesten Zufallsgeneratoren der Welt. Die ältesten Funde von Würfeln stammen ungefähr aus dem Jahr 3000 v. Chr.
Im täglichen Leben begegnet uns der Würfel in unterschiedlichen Funktionen: Spielwürfel, Zuckerwürfel, Sitzwürfel, Eiswürfel, Notizzettelwürfel …
Rund um den Würfel soll es in unserem 1. Kursraum gehen.
Viel Spaß beim Knobeln.
-
In diesem Kursraum geht es um Zahlenmauern.
Eine Mauer bezeichnet eine massive Wand aus Mauerwerk.
Mauerwerk ist ein aus natürlichen oder künstlichen Steinen gefügtes Bauteil oder Bauwerk.
Mauern haben sehr unterschiedliche Funktionen.
Es gibt Staumauern, Grenzmauern, Wehrmauern, Gefängnismauer, Stützmauern … und Zahlenmauern
-
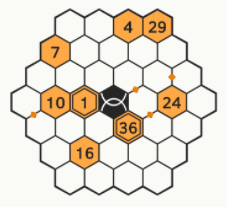
Arithmagone sind Vielecke, deren Ecken und Kanten mit Zahlen beschriftet sind.
Jede Kantenzahl ergibt sich aus der Summe der benachbarten Eckzahlen.
Du kennst Arithmagone aus deinem Mathematikbuch. Arithmagone können Rechendreiecke, Rechenvierecke oder sogar Rechenvielecke sein.
-
-
Du kennst sicher den „Zauberwürfel“ oder „Rubik’s Cube“. Er ist ein Drehpuzzle, das bereits vor 50 Jahren von dem ungarischen Bauingenieur und Architekten Ernö Rubrik erfunden wurde.
Der übliche Zauberwürfel ist in der Höhe, Breite und Tiefe in jeweils drei Lagen unterteilt, die man jeweils um ihre Mittelachse drehen kann. Die äußeren Flächen der dadurch entstehenden kleinen Würfel sind so eingefärbt, dass in der Grundposition ein Würfel mit sechs einfarbigen Flächen entsteht, zum Beispiel mit den Farben rot, blau, gelb, grün, orange und weiß.
Ziel des Puzzles ist es, den Würfel wieder in die Grundposition zu bringen, nachdem er beliebig verdreht wurde. Das Bild zeigt ein Beispiel:
Obwohl es Algorithmen, also klar beschriebene Verfahren gibt, mit denen man einen Zauberwürfel lösen kann, ist es kein leicht lösbares Puzzle. Einfacher ist es bei einem 2*2*2-Zauberwürfel, zu dem man sich auch ganz verschiedene mathematische Knobeleien ausdenken kann.
-
-
-
In dieser und einer der nächsten Aufgaben möchte ich dir Brettspiele aus anderen Ländern und alten Zeiten vorstellen. Es sind einfache Spiele, bei denen man trotzdem einen mathematischen Blick nutzen kann.
Der Schachhistoriker Harold Murray unterscheidet Brettspiele in Kriegsspiele, Jagdspiele, Wettlaufspiele, Sammelspiele sowie Aufbau- und Ausrichtungsspiele. Zur letzten Art gehört beispielsweise das bekannte Spiel Mühle. Eine sehr alte Variante des Mühlespiels heißt Kreismühle, Rundmühle oder Rota.
Rota war bereits vor etwa 3400 Jahren in Ägypten bekannt, es wurde aber auch im antiken Rom und später in vielen Ländern Europas, Asiens und Amerikas gespielt.
Gespielt wird zu zweit auf dem abgebildeten Brett. Jeder Spieler hat 3 Spielsteine seiner eigenen Farbe. Die Steine werden zunächst abwechselnd auf einen freien Knoten des Spielfeldes gelegt. (Es gibt 8 Knoten auf dem Kreis und einen auf dem Kreismittelpunkt.) Sind alle Steine ausgelegt, kann je Spielzug ein Stein der eigenen Farbe auf einen benachbarten freien Knoten verschoben werden.
Gewonnen hat, wem es als erstem gelingt, 3 Steine in einer geraden Linie anzuordnen.
-
Das Spiel Achi ist in Afrika, aber auch in Asien bekannt. Man kann es auch als kleines Mühlespiel bezeichnen, denn auch bei Achi geht es darum, 3 Steine der eigenen Farbe in eine Reihe (waagerecht, senkrecht oder diagonal) zu bringen.
Gespielt wird zu zweit auf dem abgebildeten Brett. Jeder Spieler hat 4 Spielsteine seiner eigenen Farbe. Die Steine werden zunächst abwechselnd auf einen freien Knoten des Spielfeldes gelegt. Sind alle Steine ausgelegt, kann je Spielzug ein Stein der eigenen Farbe auf einen benachbarten freien Knoten verschoben werden.
-
-
Das „Spiel des Lebens“ wurde vom Mathematiker John Horton Conway erfunden. Es ist kein richtiges Spiel, sondern ein sich selbst organisierendes System aus quadratischen Zellen, die „lebendig“ oder „tot“ sein können. Der Zustand der Zellen ändert sich Schritt für Schritt nach festen Regeln. Hat man einen Startzustand festgelegt, kann man trotzdem in der Regel nicht vorhersagen, was passiert. Oft wird man überrascht.
Das „Spiel des Lebens“ wird auf einem (gedacht) unendlich großen Gitter aus quadratischen Zellen gespielt. Für die Entwicklung der Zellen von einem Zeitpunkt zum nächsten gibt es drei Regeln, eine Überlebensregel (Ü), eine Sterberegel (S) und eine Geburtsregel (G). Diese Regeln müssen auf alle lebenden Zellen und ihre Nachbarzellen angewendet werden.
Ich erkläre dir die Regeln an einem Beispiel. Die grünen Zellen leben.
Ü: Eine lebende Zelle überlebt, wenn sie 2 oder 3 lebende Nachbarn hat.
Die Zelle L hat 2 lebende Nachbarn (G, H). Die Zelle G hat 2 lebende Nachbarn (L, H). Die Zelle H hat 3 lebende Nachbarn (L, G, I). Diese Zellen überleben.S: Eine lebende Zelle stirbt, wenn sie 0, 1, 4, 5, 6, 7 oder 8 lebende Nachbarn hat.
Die Zelle I hat nur einen lebenden Nachbarn (H). Die Zelle stirbt aus Einsamkeit.G: Eine tote Zelle wird zum Leben erweckt, wenn sie genau 3 lebende Nachbarn hat.
Die Zelle C hat genau 3 lebende Nachbarn (G, H, I). Die Zelle wird zum Leben erweckt.Nach diesen Regeln sieht das Gitter nun so aus:
Wie entwickelt sich das Leben weiter? Dazu muss man die drei Regeln wieder anwenden.
- Alle lebenden Zellen überleben, denn sie haben jeweils zwei oder drei lebende Nachbarn.
- Die Zellen B und M werden zum Leben erweckt, denn sie haben jeweils genau 3 lebende Nachbarn.
-
-
Johannes spielt gern das Steinchenspiel. Weil er es so mag, hat er sich ein „Spielbrett“ aus zwei zusammengebundenen Eierkartons selbst gebaut. Außerdem hat er 64 kleine Objekte zusammengesucht, die er als „Steinchen“ für sein Spiel benutzen kann.
Das Spielbrett besteht aus einem hellbraunen und einem grünen Karton, es hat 4 Reihen und 8 Spalten.
Man kann mit diesem Material aber nicht nur spielen, sondern auch Mathematik machen.
-
-
In diesem Kurs sind ganz unterschiedliche Aufgaben zusammengestellt, bei denen es darum geht, besondere Wege zu finden. Einige Aufgaben sind leicht, manche sind etwas knobliger. Ich wünsche dir viel Spaß dabei.
-
Zum Abschluss möchte ich dir noch einige spielerische Apps vorstellen, bei denen es darum geht, besondere Wege auszuknobeln. Bitte beachte, dass es bei diesen Apps auch Werbung gibt, eine werbefreie Version ist kostenpflichtig. Probiere die Apps deshalb beim ersten Mal nur gemeinsam mit deinen Eltern aus.
Rikudo (Number Mazes: Rikudo Puzzles)
Dieses Puzzle wurde 2015 erfunden. In einem Sechseck-Gitter sollst du einen Weg aufeinanderfolgender Zahlen finden, die in den Zellen des Gitters stehen. Einige Zahlen sind bereits zu Beginn sichtbar, andere noch verborgen. Benachbarte Zahlen sind dabei stets in benachbarten Zellen. Die Abbildung zeigt eine Beispielaufgabe, bei der ein Weg durch die Zellen von der 1 bis zur 36 gesucht ist. Wie würdest du beginnen?
Da die Zelle mit der Zahl 4 vorgegeben ist, findet sich leicht die Verbindung von 1 zur 4 als erstes Stück des gesuchten Weges. Aber wie kann es weitergehen?
Punkte auf den Gitterlinien geben den zusätzlichen Hinweis, dass in den angrenzenden Zellen benachbarte Zahlen stehen. Der gesuchte Weg muss also über die markierte Strecke verlaufen.
Hashi (Brücken)
Hashi ist ein Brückenspiel.
In einem rechteckigen Gitter sind „Inseln“ angeordnet, die du durch Brücken so miteinander verbinden sollst, dass jede Insel von jeder anderen Insel erreichbar ist. Die Brücken müssen waagerecht oder lotrecht verlaufen und dürfen sich nicht kreuzen. Außerdem dürfen zwischen zwei Inseln höchstens zwei Brücken sein. Das alles wäre leicht zu realisieren, wenn nicht zusätzlich für jede Insel vorgegeben wäre, wie viele Brücken es dorthin geben darf.
Cube Connect
Auf einem Würfel, von dem man drei Seiten sehen und nutzen kann, sind verschiedenfarbige Punkte angeordnet, von jeder Farbe zwei. Die gleichfarbigen Punkte sollst du auf der Würfeloberfläche durch Streckenzüge verbinden, bei denen die einzelnen Strecken parallel zu den Würfelkanten verlaufen müssen. Knoblig wird es dadurch, dass sich die Streckenzüge nicht kreuzen dürfen. Du musst deshalb gut vorausschauen und trainierst dabei auch dein Vorstellungsvermögen.
-
Im Zirkus Leonardo treten nicht nur Artisten, Clowns und Zauberer auf, an vielen Stellen gibt es auch einiges zu knobeln und zu rechnen. Ich wünsche dir viel Spaß dabei.
-
-
-
„Mastermind“ ist ein Logikspiel für zwei Personen. Der erste Spieler – der Code-Setzer – denkt sich einen geheimen Code aus 4 Farben aus. Der zweite Spieler – der Code-Knacker – muss versuchen, diesen so schnell wie möglich zu erraten. Zu jedem Rateversuch muss der Code-Setzer Rückmeldungen geben, die der Code-Knacker für den nächsten Versuch nutzen kann.
Die folgende Abbildung zeigt an einem Beispiel, wie das Spiel funktioniert.
- Der Code-Setzer kann aus den Farben rot, grün, blau, gelb, lila und braun auswählen und einen Code mit 4 Farben zusammenstellen. Dabei können Farben auch mehrfach auftreten. Im Beispiel wählt er lila-gelb-blau-lila. Natürlich darf der Code-Knacker den Code nicht sehen.
- Der Code-Knacker gibt einen Tipp ab. Er wählt rot-gelb-lila-grün.
- Der Code-Setzer vergleicht den Tipp mit seinem Code: Eine Farbe (lila) ist richtig, aber an der falschen Stelle, dafür gibt es weiß als Rückmeldung. Eine weitere Farbe (gelb) ist richtig und sogar an der richtigen Stelle, dafür gibt es schwarz. Die anderen beiden Farben (rot, grün) sind falsch, dafür gibt es keine Farbe. (Die Reihenfolge der Rückmeldungen ist beliebig.)
- Der Code-Knacker weiß jetzt, dass in seinem Tipp eine Farbe richtig ist und an der richtigen Stelle, eine andere Farbe ist richtig, muss aber noch an eine andere Stelle verschoben werden. Die beiden anderen Farben kommen im Code des Code-Setzers nicht vor. Davon ausgehend kann der Code-Knacker den nächsten Tipp abgeben, zu dem der Code-Setzer wieder mittels weiß und schwarz Rückmeldungen gibt usw.
Wenn der Code geknackt wurde oder alle Versuche verbraucht sind, werden die Rollen von Code-Setzer und Code-Knacker getauscht.
Das Spiel gibt es in verschiedenen Varianten. Beispielsweise kann die Anzahl der Farben verändert werden oder die Länge des Farbcodes. Außerdem kann man auch festlegen, dass jede Farbe höchstens einmal im Code vorkommen darf.
Das Spiel gibt es als Brettspiel oder als App für Computer oder Mobiltelefon. Beispielsweise kannst du es hier in der Rolle des Code-Knackers spielen: http://www.steyrerbrains.at/spiele/Mastermind/.
Natürlich kann man auch Mathematik damit machen.
-
„Mastermind“ ist ein Logikspiel für zwei Personen. Der erste Spieler – der Code-Setzer – denkt sich einen geheimen Code aus 4 Farben aus. Der zweite Spieler – der Code-Knacker – muss versuchen, diesen so schnell wie möglich zu erraten. Zu jedem Rateversuch muss der Code-Setzer Rückmeldungen geben, die der Code-Knacker für den nächsten Versuch nutzen kann.
Die folgende Abbildung zeigt an einem Beispiel, wie das Spiel funktioniert.
- Der Code-Setzer kann aus den Farben rot, grün, blau, gelb, lila und braun auswählen und einen Code mit 4 Farben zusammenstellen. Dabei können Farben auch mehrfach auftreten. Im Beispiel wählt er lila-gelb-blau-lila. Natürlich darf der Code-Knacker den Code nicht sehen.
- Der Code-Knacker gibt einen Tipp ab. Er wählt rot-gelb-lila-grün.
- Der Code-Setzer vergleicht den Tipp mit seinem Code: Eine Farbe (lila) ist richtig, aber an der falschen Stelle, dafür gibt es weiß als Rückmeldung. Eine weitere Farbe (gelb) ist richtig und sogar an der richtigen Stelle, dafür gibt es schwarz. Die anderen beiden Farben (rot, grün) sind falsch, dafür gibt es keine Farbe. (Die Reihenfolge der Rückmeldungen ist beliebig.)
- Der Code-Knacker weiß jetzt, dass in seinem Tipp eine Farbe richtig ist und an der richtigen Stelle, eine andere Farbe ist richtig, muss aber noch an eine andere Stelle verschoben werden. Die beiden anderen Farben kommen im Code des Code-Setzers nicht vor. Davon ausgehend kann der Code-Knacker den nächsten Tipp abgeben, zu dem der Code-Setzer wieder mittels weiß und schwarz Rückmeldungen gibt usw.
Wenn der Code geknackt wurde oder alle Versuche verbraucht sind, werden die Rollen von Code-Setzer und Code-Knacker getauscht.
Das Spiel gibt es in verschiedenen Varianten. Beispielsweise kann die Anzahl der Farben verändert werden oder die Länge des Farbcodes. Außerdem kann man auch festlegen, dass jede Farbe höchstens einmal im Code vorkommen darf.
Das Spiel gibt es als Brettspiel oder als App für Computer oder Mobiltelefon. Beispielsweise kannst du es hier in der Rolle des Code-Knackers spielen: http://www.steyrerbrains.at/spiele/Mastermind/.
Natürlich kann man auch Mathematik damit machen.
-
-
-
Frage gern deine Eltern, ob du Hashi auf einem Handy oder Tablet spielen darfst. Es gibt verschiedene Schwierigkeitsstufen. Viel Spaß!
Play Store:
App Store:
-
Frage gern deine Eltern, ob du Hashi auf einem Handy oder Tablet spielen darfst. Es gibt verschiedene Schwierigkeitsstufen. Viel Spaß!
Play Store:
App Store:
