Felder, Figuren, Stellungen

Felder

Felder auf dem Schachbrett können auf drei verschiedene Arten bezeichnet werden:

"b3", [5,1], 41 bezeichnen alle das selbe, in der Abbildung markierte Feld:

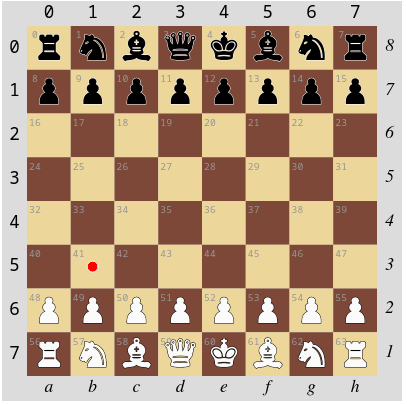
Die untere und die rechte Achsenbeschriftung bezieht sich auf die klassische Notation.

Die linke und die obere Achsenbeschriftung bezieht sich auf die zweidimensionalen Koordinaten.
Hier gilt: Die erste Koordinate gehört zur senkrechten Achse (in der Schachsprache: die Reihe)
Die zweite Koordinate gehört zur waagerechten Achse (in der Schachsprache: die Linie)

Die eindimensionalen Koordinaten erhaltet ihr, wenn ihr die Felder, bei 0 beginnend, von oben links durchzählt.
(Damit ihr euch die Zählerei spart, stehen in unserer Darstellung des Brettes die Nummern auf den Feldern.)

Die eindimensionalen Koordinaten sind die "Muttersprache" unseres Programms. 

Das heißt alle Berechnungen von gültigen Zügen, die Ausführung von Zügen, die Angaben markierter Felder etc. werden mit eindimensionalen Koordinaten durchgeführt. Wenn also irgendwo im Code feld steht, ist damit immer eine eindimensionale Koordinate gemeint.

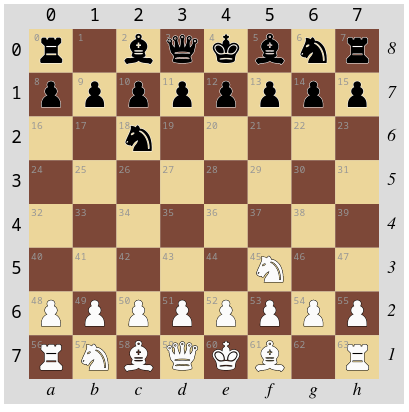
In dieser Stellung liefert der Funktionsaufruf...

logik.gueltigeZielfelder(45, spielzustand)

 

...folgenden Wert, also die gültigen Züge des Springers auf Feld 45:

[62, 28, 30, 35, 39]

 

Entsprechend können wir die markieren mit:

gui.zeichne(spielzustand, [62, 28, 30, 35, 39])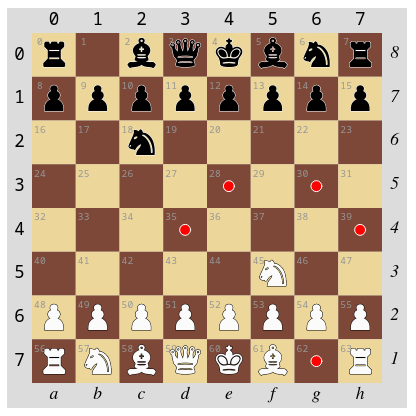 

 

Das sieht dann so aus:

 

Einen Zug ausführen könntet ihr so:

spielzustand = spielzustand.zugUngeprueft(45, 35)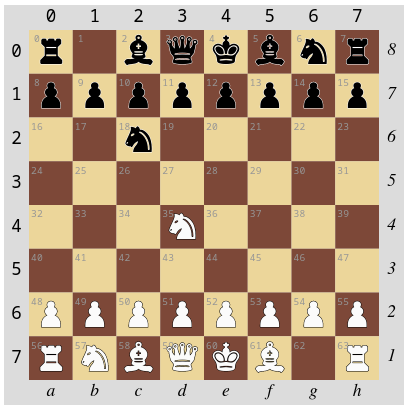 

 

Mit dem Ergebnis:

 

Falls wir mal andere Bezeichnungen brauchen (zum Beispiel, um Partien in einer Textdatei zu speichern), können wir die Funktionen in der Datei umwandlungen.js nutzen:

 

umwandlungen.index2dZuNotation([3, 4])
//=> "e5"

 

umwandlungen.notationZuIndex2d("e5")

//=> [3, 4]

 

umwandlungen.index1dZuNotation(28)
//=> "e5"

 

umwandlungen.notationZuIndex1d("e5")

//=> 28

 

Figuren

Figuren werden durch ganze Zahlen repräsentiert.
Negative Zahlen stehen für schwarze Figuren:
-1 Bauer, 
-2 Springer,
-3 Läufer,
-4 Turm,
-5 Dame,
-6 König.
0 steht für ein leeres Feld.
Positive Zahlen stehen für weiße Figuren:
1 Bauer,
2 Springer,
3 Läufer,
4 Turm,
5 Dame,
6 König.

Damit wir nicht jedes mal nachschauen müssen, welche Zahl für welche Figur steht, können wir auch die folgenden Bezeichner verwenden:

BS
SS
LS
TS
DS
KS

BW
SW
LW
TW
DW
KW

In dieser Stellung liefert spielzustand.figur(35) den Wert -2, weil auf dem Feld ein schwarzer Springer steht.

Stellungen

Wir können Stellungen als zweidimensionale Arrays darstellen (so wie wir das in der Datei stellungen.js machen):

[[TS, SS, LS, DS, KS, LS, SS, TS],
 [BS, BS, BS, BS, BS, BS, BS, BS],
 [ 0,  0,  0,  0,  0,  0,  0,  0],
 [ 0,  0,  0,  0,  0,  0,  0,  0],
 [ 0,  0,  0,  0,  0,  0,  0,  0],
 [ 0,  0,  0,  0,  0,  0,  0,  0],
 [BW, BW, BW, BW, BW, BW, BW, BW],
 [TW, SW, LW, DW, KW, LW, SW, TW]]

Aber auch für Stellungen gilt: Die eindimensionale Darstellung ist die "Muttersprache" unseres Programms.

spielzustand.felder liefert (mit ein paar Tricks) dieses Ergebnis:

[-4, -2, -3, -5, -6, -3, -2, -4, -1, -1, -1, -1, -1, -1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, ...]

Auch hier gibt es Übersetzungfunktionen:

umwandlungen.array2dZuArray1d(array2d)

umwandlungen.array1dZuArray2d(array1d)