Thema 2: Die Rechnung bitte! - Lösungen
| Website: | Webakademie Sachsen-Anhalt |
| Kurs: | Lehrerzimmer MINTzi |
| Buch: | Thema 2: Die Rechnung bitte! - Lösungen |
| Gedruckt von: | Gast |
| Datum: | Freitag, 13. März 2026, 02:22 |
Beschreibung
Du kannst die Lösungen zum Durchgang "Die Rechnung bitte!" hier in der Webakademie einsehen. Klicke dich dazu durch das nachfolgende "Buch".
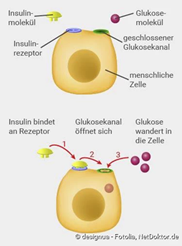
Lösung 1: Hilfe, ich brauche Zucker - die Zuckerkrankheit Diabetes
(A) Lösung nur beispielhaft:
Quellen:
Schwarz- Video 1: https://youtu.be/RiCzvzPL72E
Blau- https://www.netdoktor.de/krankheiten/diabetes-mellitus/
https://www.netdoktor.de/symptome/hypoglykaemie-unterzuckerung/
Hellblau- https://www.gesundheitsinformation.de/diabetes-typ-1.2196.de.html
Grün- https://www.diabetes-ratgeber.net/Diabetes-Typ-2
Orange- https://lehrerfortbildung-bw.de/u_matnatech/bio/gym/bp2004/fb4/2_gen/blau_weiss/11_her4/
|
Arten von Diabetes |
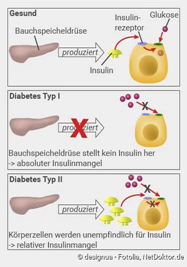
Diabetes Typ 1 |
Diabetes Typ 2 |
|---|---|---|
|
Ursachen |
-gestörte Blutzuckerregulation (Stoffwechselerkrankung)
|
|
|
-Bauchspeicheldrüse ist gestört |
-Körperzellen zunehmend unempfindlich gegen Insuline Insulinresistenz löst einen relativen Insulinmangel aus (vorhandenes Insulin kann nicht/nur unzureichend wirken) -begünstigende Faktoren: Übergewicht, Adipositas, Rauchen, Bewegungsmangel |
|
|
Verlauf |
-es werden Autoantikörper gebildet -Autoantikörper zerstören Beta-Zellen -der Körper kann kein Insulin mehr produzieren - zeitlebens Insulin spritzen - dauerhafte Überzuckerung kann zu Schäden an vielen Organe oder auch zu Schäden an den Blutgefäßen, die das Gewebe versorgen, führen (extreme Folgen von Blutgefäßschädigungen sind z.B. Erblindung oder Nierenversagen)
|
-Körper nimmt nicht genug Glukose in die Zellen auf→ Glukose bleibt im Blut→ Blutzuckergehalt ist sehr hoch→ Körper produziert immer mehr Insulin→ nach Überproduktion irgendwann Überbelastung→ keine Produktion mehr von Insulin -kann teilweise durch Einnahme von Medikamenten geregelt werden; es erfolgen auch Insulinspritzungen - Änderungen beim Lebensstil können anfangs reichen (Sport, gesunde Ernährung,..)
-wichtigste Folgeerkrankungen: Herzinfarkt, Schlaganfall, Nierenschwäche, Netzhautschäden und Nervenstörungen |
|
Herstellungsmöglichkeiten von Insulin |
-Gewinnung des Insulin-Gens und Herstellung von Insulin über eine copy-DANN (über gentechnisch veränderte Bakterien z.B. Escherichia coli (E.coli) ) - aus der Bauchspeicheldrüse (Pankreas) eines Schweins |
|
|
Allgemeine Infos |
-oft auch als Zuckerkrankheit bezeichnet |
|
|
-Ursache ist eine Autoimmunerkrankung - etwa 200.000 Menschen in Deutschland haben einen Typ-1-Diabetes, darunter etwa 30.000 Kinder und Jugendliche bis 19 Jahre - pro Jahr erkranken etwa 2 von 10.000 Kindern neu daran |
-häufigste Form des Insulinmangels -überwiegender Anteil (über 90 Prozent) aller rund 7Mio. Diabetiker*innen -in der Vergangenheit als „Altersdiabetes“ bezeichnet |
|
Der Unterschied von Diabetes Typ 1 und Typ 2 ist, dass Typ 2 eine Insulinresistenz zugrunde liegt.

Wenn davon ausgegangen wird, dass Milch ungefähr eine Dichte zwischen 1,028 bis 1,035 Kg pro Liter, je nach Fettgehalt hat.
(C) Eine starke Überzuckerung löst die typischen Symptome wie Durst, häufiges Wasserlassen und lähmende Müdigkeit aus. Diese Beschwerden lassen sich durch die Gabe von Insulin schnell lindern. Ist der Blutzuckerspiegel sehr stark erhöht, kann es auch zu Bewusstseinsstörungen bis hin zur Bewusstlosigkeit (diabetisches Koma) kommen. Ein diabetisches Koma durch eine extreme Überzuckerung ist heute sehr selten. Vor der Entwicklung der Insulintherapie im Jahr 1922 war es eine unvermeidliche Krankheitsfolge und führte zum Tod. Menschen, die an Typ-1-Diabetes erkrankten, überlebten deshalb nicht lange.
Wird sich zum Beispiel zu viel Insulin gespritzt, kann man in eine starke Unterzuckerung fallen. Auf den Mangel reagiert der Körper mit Stresssymptomen wie Schwitzen, Herzrasen und Zittern. Der Körper reagiert mit Krampfanfälle und Lähmungen, Atem- und Kreislaufstörungen sowie Bewusstlosigkeit. Manchmal enden solche schweren Hypoglykämien im Koma. Eine schwere Unterzuckerung ist sogar lebensbedrohlich.
| Frühstück | Mittag | Abendessen |
|---|---|---|
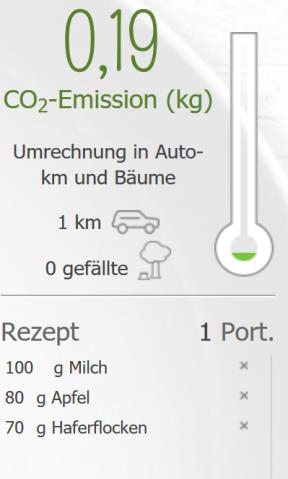 |
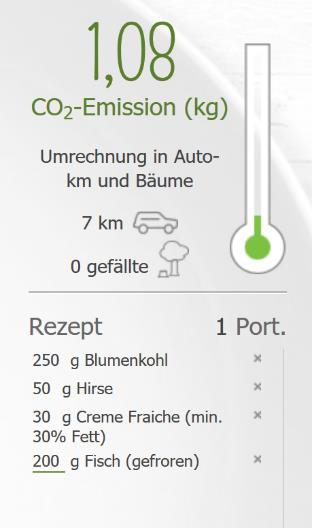 |
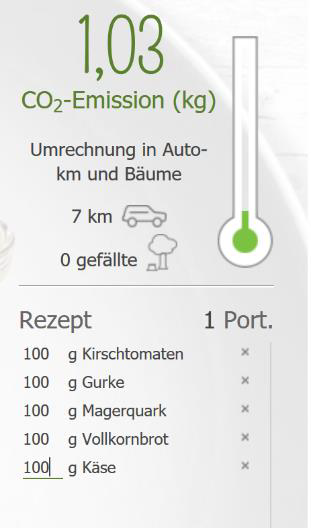 |
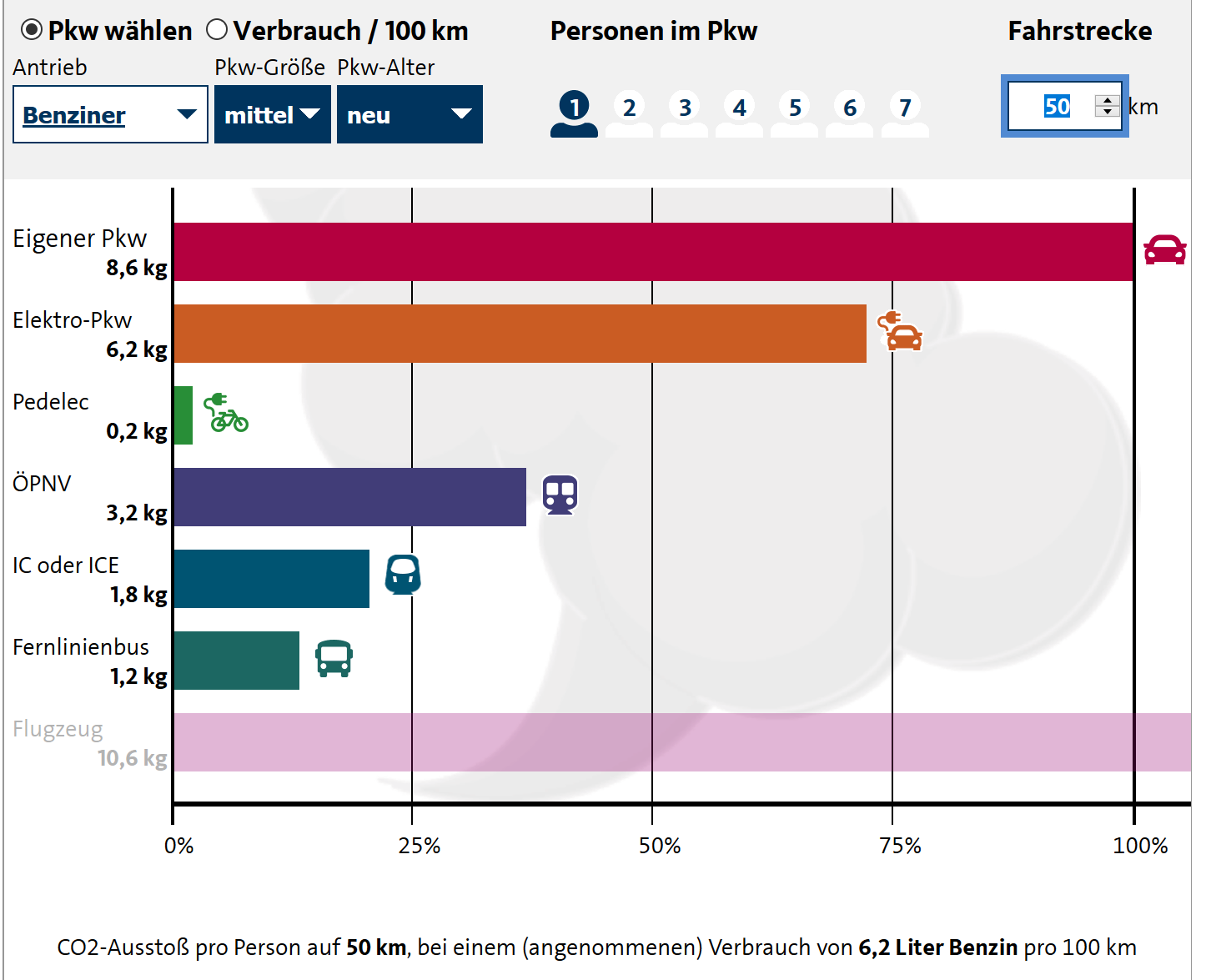
Lösung 3: Wurzeln ziehen im Gemüsebeet
Der Flächeninhalt eines rechteckigen Beetes ist 𝐴=(𝑎;𝑏)=𝑎∗𝑏, wobei 𝑎 die Breite und 𝑏 die Höhe bzw. Länge des Rechtecks ist.
Würden nicht alle Ecken des Rechtecks auf der Grundstückslinie (Grundstücksgrenze) liegen, dann lässt sich das Rechteck noch weiter vergrößern. Damit muss der rechts oben liegende Eckpunkt des Rechtecks, das wir bestimmen wollen, auf dem Graphen der Funktion 𝑓 liegen. Demnach können wir den Flächeninhalt schreiben als:
𝑎∗𝑏=𝑎∗𝑓(𝑎)=𝑎∗(−130∗𝑎2∗+30)
Es ist wichtig zu bemerken, dass der Flächeninhalt 𝐴 nur noch von der Breite 𝑎 des Rechtecks abhängt, sodass wir anstelle von 𝐴(𝑎;𝑏) nur noch 𝐴(𝑎) betrachten können. Dabei ist 𝐴(∗)die Flächeninhaltsfunktion, die wir maximieren wollen. Dazu bestimmen wir die erste Ableitung von 𝐴(𝑎)=−130∗𝑎3+30. Es gilt:
𝐴′(𝑎)=3∗−130∗𝑎2=−110∗𝑎2 und aus 𝐴′(𝑎)=−110∗𝑎2=0 folgt
𝑎1,2=∓√300≈∓17,32
Dabei ist natürlich nur die Breite 𝑎2=17,32 zulässig, denn 𝑎1 ist negativ. Somit kann dies keine Seitenlänge sein.
Um zu überprüfen, ob 𝑎2 wirklich maximal ist, bestimmen wir (das Vorzeichen von) 𝐴′′(𝑎2).
Es gilt: 𝐴′′(𝑎)= −15∗𝑎 und somit 𝐴′′(𝑎2)=𝐴′′(17,32)=−15∗17,32= −3,464<0
Damit ist 𝑎2 eine Maximalstelle.
Somit hat das Rechteck die Breite 𝑓(𝑎2)=𝑓(17,32)=(−130∗17,322∗+30)≈20
und einen Flächeninhalt von 𝐴(𝑎2)= 𝑎2∗𝑓(𝑎2)=17,32∗20=346,41
Lösung 4: Gut vernetzt
Ja, die Bäuerin muss ein Netz zerschneiden. Dazu stellen wir uns das Beet wie ein Schachbrett vor. Wir zerlegen das Beet in 36 Teile, die wir abwechselnd schwarz und weiß färben. Somit sind insgesamt 18 Felder schwarz und 16 Felder weiß. (Zwei weiße Felder sind in der Skizze in der Aufgabe rot. Dies sind die unbrauchbaren Teile des Beetes.)
Egal wie man ein Netz spannt, es überdeckt genau zwei Felder. Ein Feld ist schwarz und das andere ist weiß. Insgesamt braucht man also genau 16 Netze, um die 16 weißen Felder zu überdecken. Dabei werden natürlich auch gleichzeitig 16 schwarze Felder überdeckt.
Es bleiben aber genau 2 schwarze Felder über. Da diese nicht nebeneinander liegen, muss das 17. Netz zerschnitten werden.
0=𝑧𝑛−𝛼∗𝑧𝑛−𝛽∗𝛾∗𝑧𝑛−1=𝑧𝑛−1∗(𝑧2−𝛼∗𝑧−𝛾∗𝛽)
Produkte verschwinden, wenn mindestens einer der Faktoren verschwindet und da 𝑧≠0 folgt 𝑧2−𝛼∗𝑧−𝛾∗𝛽=0.
0=𝑐1∗𝑧10+𝑐2∗𝑧20=𝑐1+𝑐2 , somit gilt 𝑐1=−𝑐2.
Wir setzen dies in die Gleichung 𝑋1=1 ein und erhalten: 1=𝑐1∗ 𝑧1+𝑐2∗𝑧2=𝑐1∗ 𝑧1−𝑐1∗𝑧2= 𝑐1∗(𝑧1−𝑧2)=𝑐1∗(12∗√𝛼2+4∗𝛽∗𝛾−−12∗√𝛼2+4∗𝛽∗𝛾)=𝑐1∗√𝛼2+4∗𝛽∗𝛾
Die Dreiecksungleichung liefert |𝑧2|=|𝛼2−12√𝛼2+4∗𝛽∗𝛾| ≤|𝛼2|+|12√𝛼2+4∗𝛽∗𝛾| =𝛼2+ 12√𝛼2+4∗𝛽∗𝛾| =𝑧1
Wir haben also |𝑧2|=𝑧1.
Falls |𝑧2|=𝑧1, gilt entweder 𝑧2=𝑧1 oder 𝑧2=𝑧1
Aus 𝑧2=𝑧1 folgt 𝛼=0
Aus 𝑧2=−𝑧1 folgt √𝛼2+4∗𝛽∗𝛾=0
Aus (i) wissen wir |𝑧2|<𝑧1 und daher ist |𝑧2𝑧1|<1, also 𝑧2𝑧1→0 𝑓ü𝑟 𝑛→∞
Für 𝑧1>1 ist 𝑧1→∞,𝑧1<1 folgt 𝑧1𝑛→0 , da 𝑧1>0.
Gleiches muss wegen (ii) auch für 𝑋𝑛 gelten. Für den
Fall 𝑧1=1 𝑖𝑠𝑡 𝑧1𝑛=1 𝑓ü𝑟 𝑗𝑒𝑑𝑒𝑠 𝑛.
√𝛼2+4∗𝛽∗𝛾 =−𝛼 |(…)2
➔ 𝛽∗𝛾=1−𝛼
Also 𝛼=1−𝛽∗𝛾.
Für den Fall 𝛾=12 und 𝛼=𝛽 erhalten wir 𝛼=23.