Aufgabe 5: Der ganz normale Corona-Wahnsinn (Zusatzaufgabe)
Abschlussbedingungen
Foto: https://www.pexels.com/de-de/foto/weisse-rote-und-blaue-blutenblatter-3993212/
In den vergangenen Jahren hat uns alle ein Virus sehr beschäftigt, das Coronavirus. Vielleicht warst du sogar schon selbst davon betroffen? Doch auch, wenn du bisher Glück hattest und von der Krankheit verschont geblieben bist, hat sich dein Leben sicher verändert. Begriffe wie Inzidenz und Inkubationszeit bestimmen nun den Alltag. Auch in der epidemiologischen Forschung gehören diese Begriffe zur Tagesordnung. Die Erfassung der Inkubationszeit neuer Krankheiten stellt für die Forschenden ein wiederkehrendes Problem dar. Diese Zeit beschreibt die Dauer zwischen der Ansteckung und dem Auftreten erster Symptome. Sie unterscheidet sich von Patient*in zu Patient*in erheblich.
Deswegen lässt sie sich als zufällige Größe T auffassen, die wie beispielsweise das Körpergewicht des Menschen einer gewissen Verteilung entspricht. Die Inkubationszeit kann dabei durch eine logarithmische Normalverteilung beschrieben werden, wie die Erfahrung mit anderen Viren gezeigt hat. Die zugehörige Funktion lautet für alle Inkubationszeiten t:
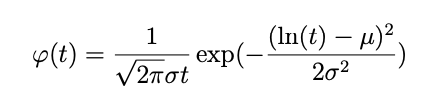
Die beiden reellen Zahlen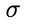
und 
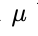beschreiben Parameter, die von der Krankheit abhängig sind.
Die folgende Abbildung zeigt die Graphen von Funktionen verschiedener logarithmisch-normalverteilter Zufallsgrößen.
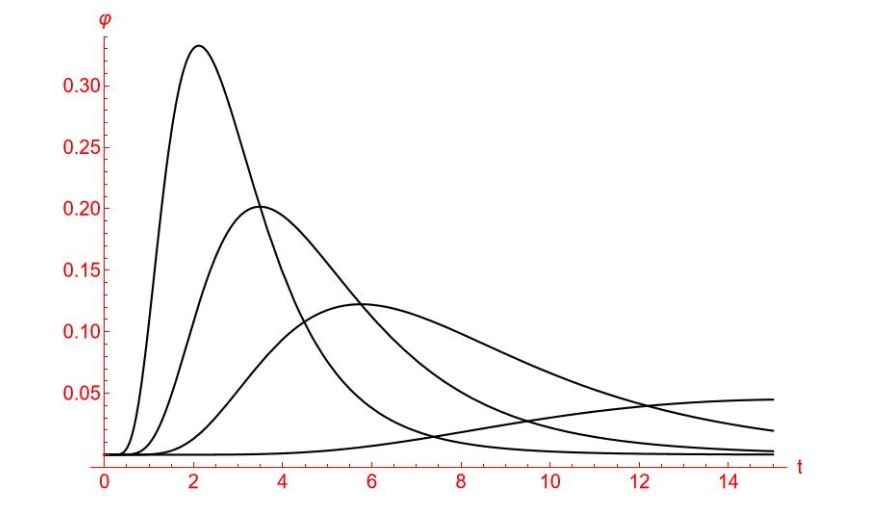
Foto: Experimente-Werkstatt Mathematik
Um die Wahrscheinlichkeit zu berechnen, dass eine logarithmisch-normalverteilte Zufallsgröße T Werte \( \leq \) einer bestimmten Zeit t annimmt, lässt sich folgender Zusammenhang zur Verteilungsfunktion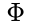
der Standardnormalverteilung verwenden:
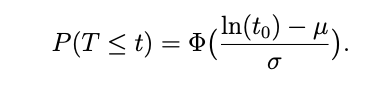
In einem wissenschaftlichen Artikel geben britische Forscher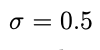
für die Delta-Variante von Covid 19 an, ohne jedoch einen Wert für 
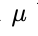mitzuteilen. Wir wollen 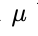schätzen, damit verlässliche Aussagen zur Inkubationszeit gemacht werden können. Eine Stichprobe bei zehn Patient*innen ergab folgende Inkubationszeiten (in Tagen):
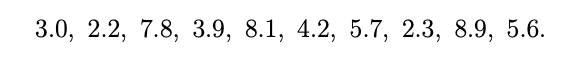
Der Erwartungswert E(T) einer Zufallsgröße T beschreibt die Zahl, welche im Mittel angenommen wird (arithmetisches Mittel). Für logarithmisch-normalverteilte Zufallsgrößen ist
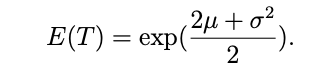
(A) Berechne das arithmetische Mittel der Stichprobe. Mit dieser Näherung für den Erwartungswert lässt sich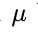
abschätzen, wenn 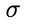wie oben angenommen wird.
(B) Stelle den Graphen der Funktion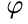
für den ermittelten Parameter in einem Koordinatensystem dar. Betrachte dabei den Zeitraum von 0 bis 15 Tagen.
(C) Wie groß ist die Wahrscheinlichkeit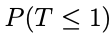
, dass eine Person bereits einen Tag nach der Infektion Symptome entwickelt?
Foto: https://www.pexels.com/de-de/foto/weisse-rote-und-blaue-blutenblatter-3993212/
In den vergangenen Jahren hat uns alle ein Virus sehr beschäftigt, das Coronavirus. Vielleicht warst du sogar schon selbst davon betroffen? Doch auch, wenn du bisher Glück hattest und von der Krankheit verschont geblieben bist, hat sich dein Leben sicher verändert. Begriffe wie Inzidenz und Inkubationszeit bestimmen nun den Alltag. Auch in der epidemiologischen Forschung gehören diese Begriffe zur Tagesordnung. Die Erfassung der Inkubationszeit neuer Krankheiten stellt für die Forschenden ein wiederkehrendes Problem dar. Diese Zeit beschreibt die Dauer zwischen der Ansteckung und dem Auftreten erster Symptome. Sie unterscheidet sich von Patient*in zu Patient*in erheblich.
Deswegen lässt sie sich als zufällige Größe T auffassen, die wie beispielsweise das Körpergewicht des Menschen einer gewissen Verteilung entspricht. Die Inkubationszeit kann dabei durch eine logarithmische Normalverteilung beschrieben werden, wie die Erfahrung mit anderen Viren gezeigt hat. Die zugehörige Funktion lautet für alle Inkubationszeiten t:
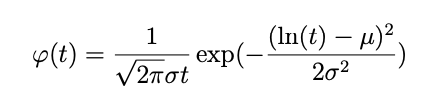
Die beiden reellen Zahlen
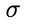und 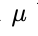beschreiben Parameter, die von der Krankheit abhängig sind. Die folgende Abbildung zeigt die Graphen von Funktionen verschiedener logarithmisch-normalverteilter Zufallsgrößen.
Foto: Experimente-Werkstatt Mathematik
Um die Wahrscheinlichkeit zu berechnen, dass eine logarithmisch-normalverteilte Zufallsgröße T Werte \( \leq \) einer bestimmten Zeit t annimmt, lässt sich folgender Zusammenhang zur Verteilungsfunktion
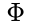der Standardnormalverteilung verwenden: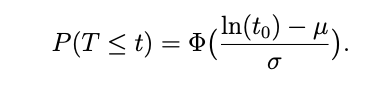In einem wissenschaftlichen Artikel geben britische Forscher
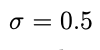für die Delta-Variante von Covid 19 an, ohne jedoch einen Wert für 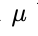mitzuteilen. Wir wollen 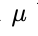schätzen, damit verlässliche Aussagen zur Inkubationszeit gemacht werden können. Eine Stichprobe bei zehn Patient*innen ergab folgende Inkubationszeiten (in Tagen):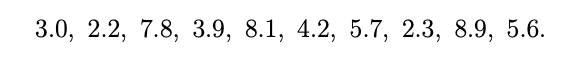Der Erwartungswert E(T) einer Zufallsgröße T beschreibt die Zahl, welche im Mittel angenommen wird (arithmetisches Mittel). Für logarithmisch-normalverteilte Zufallsgrößen ist
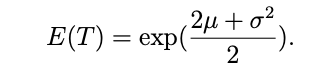
(A) Berechne das arithmetische Mittel der Stichprobe. Mit dieser Näherung für den Erwartungswert lässt sich
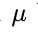abschätzen, wenn 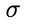wie oben angenommen wird.(B) Stelle den Graphen der Funktion
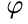für den ermittelten Parameter in einem Koordinatensystem dar. Betrachte dabei den Zeitraum von 0 bis 15 Tagen.(C) Wie groß ist die Wahrscheinlichkeit
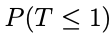, dass eine Person bereits einen Tag nach der Infektion Symptome entwickelt?
